神经网络要点理解

1 损失函数及其正则化

一个未经正则化的神经网络损失函数为：

\begin{equation} \label{eq:1} J(\Theta) = \frac{1}{m} \sum_{i=1}^{m} \sum_{k=1}^{K} \big[ - y_{k}^{(i)}\log ((h_{\theta}(x^{(i)}))_{k}) - (1-y_{k}^{(i)})\log (1- (h_{\theta}(x^{(i)}))_{k} ) \big] \end{equation}

其中\(h_{\theta}(x)\)的计算如下：

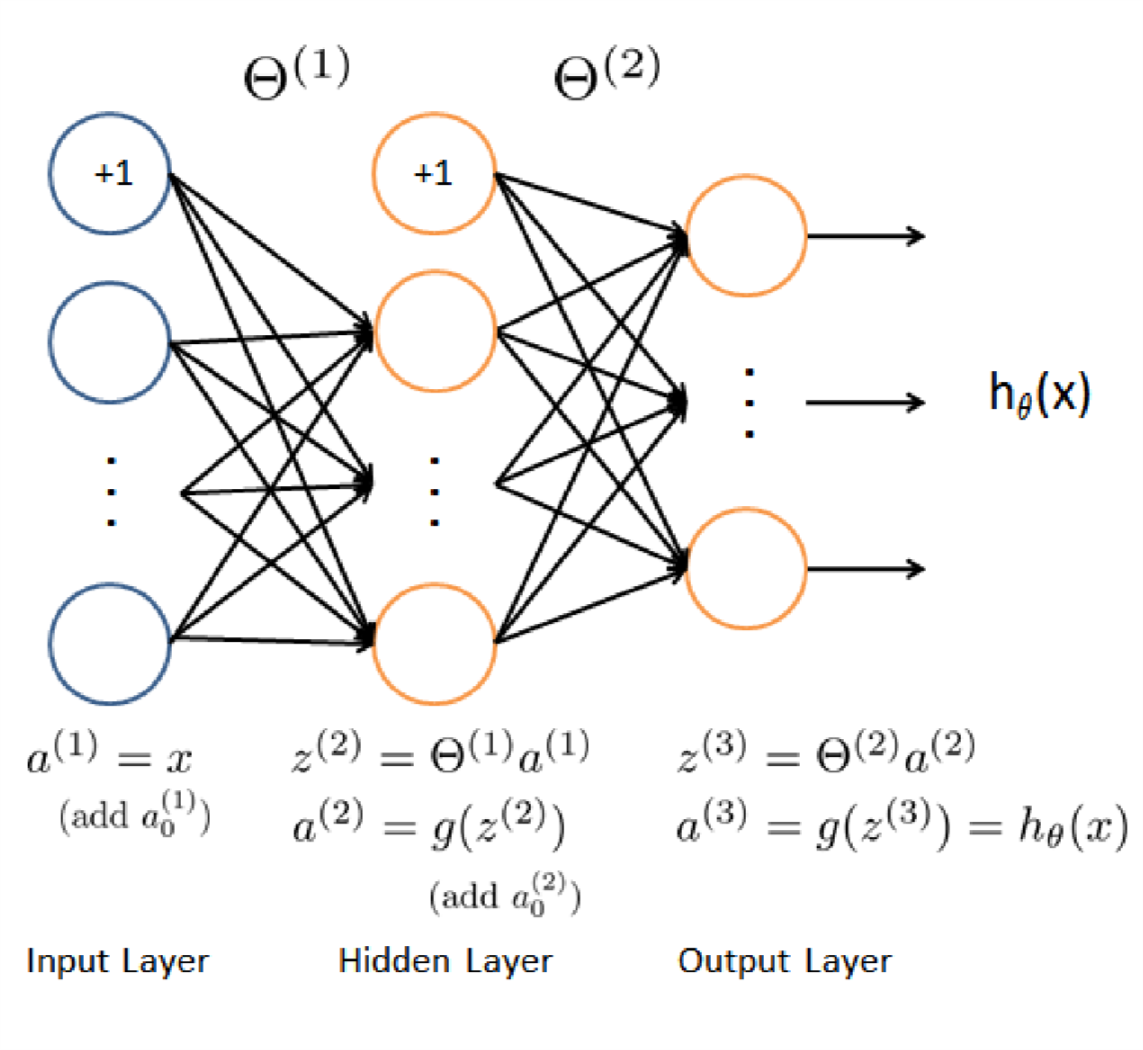
此处\(L=3\).

针对上面的公式，我们有\(x^{(i)}\)表示第\(i\)个样本的矢量，这个矢量的大小是\(400\times 1\)。\(h_{\theta}(x^{(i)})_{k}\)表示第\(i\)个输入在第\(K\)个类上的输出。每一个输入样本\(x^{(i)}\)都会在神经网络的输出层产生\(K\)个输出，表示\(x^{(i)}\)属于这\(K\)个类中每个类的可能性。

当我们给定\(\Theta_{1}\)，\(\Theta_{2}\)时，我们可以根据上图来计算每一个\(h_{\theta}(x^{i})\)，进而根据\(J(\Theta)\)的公式来计算损失函数。

注意在计算的过程中，我们遇到的一些矩阵(从上图到\(J(\Theta)\)的计算过程中遇到的矩阵)的维度为：

矩阵	维度
\(a^{(1)}\)	\(5000\times 401\)
\(\Theta^{(1)}\)	\(25\times 401\)
\(z^{(2)}\)	\(25\times 5000\)
\(a^{(2)}\)	\(26\times 5000\)
\(\Theta^{(2)}\)	\(10\times 26\)
\(z^{(3)}\)	\(10\times 5000\)
\(a^{(3)}\)	\(10\times 5000\)
\(Y\)	\(10\times 5000\)

其中\(a^{(1)}\) 为添加了\(a_{0}^{(1)}\)后的矩阵；\(a^{(2)}\)为添加了\(a_{0}^{(2)}\)后的矩阵；\(Y\)为把1,2,…,10映射为矢量后的矩阵。

\(J(\Theta)\)计算的是5000个用户在10个类上的cost之和。所以式~(\ref{eq:1})的方括号中如果是矩阵的话应该是一个\(10\times 5000\)的矩阵。

计算\(J(\Theta)\)的部分代码为：

a1 = [ones(m,1) X];
z2 = Theta1*a1';
a2 = 1./(1 + exp(-z2));
a2 = [ones(1,size(a2,2));a2];%add a_0^(2)
z3 = Theta2 * a2;

a3 = 1./(1 + exp(-z3));%10X5000

temp = eye(num_labels);
Y = temp(:,y);
J = (Y .* log(a3) + (1-Y).* log(1-a3))./m;
J = -1*sum(sum(J));

注意为了支持任何大于\(K>3\)的分类，代码中不允许出现任何的magic number。比如：

temp = eye(num_labels);

就不能写成：

temp = eye(10);

虽然在这个例子中 num_labels=10 magic number 也是不被允许的。

接下来是正则项的计算：

\begin{equation} \label{eq:2} \frac{\lambda}{2m} \big [ \sum_{j=1}^{25}\sum_{k=1}^{400} (\Theta_{j,k}^{(1)})^{2} + \sum_{j=1}^{10}\sum_{k=1}^{25}(\Theta_{j,k}^{2})^{2} \big] \end{equation}

同样magic number是不被允许的。

2 后向传递算法

后向传递算法的步骤为：

给定一个训练样本\(x^{(t)},y^{(t)}\) 首先计算前向过程，直到输出\(h_{\theta}(x)\)
对每个层\(l\)的每个节点\(j\)，计算误差项\(\delta_{j}^{(l)}\)，这个误差项用来度量这个节点对输出负多大的“责任”；
对于输出节点，我们直接计算网络的activation输出和真实的目标值之间的差即可。用这个差值作为\(\delta_{j}^{(3)}\)，对于隐藏的层，计算\(\delta_{j}^{(l)}\)时需要加权考虑层\(l+1\)上的错误。

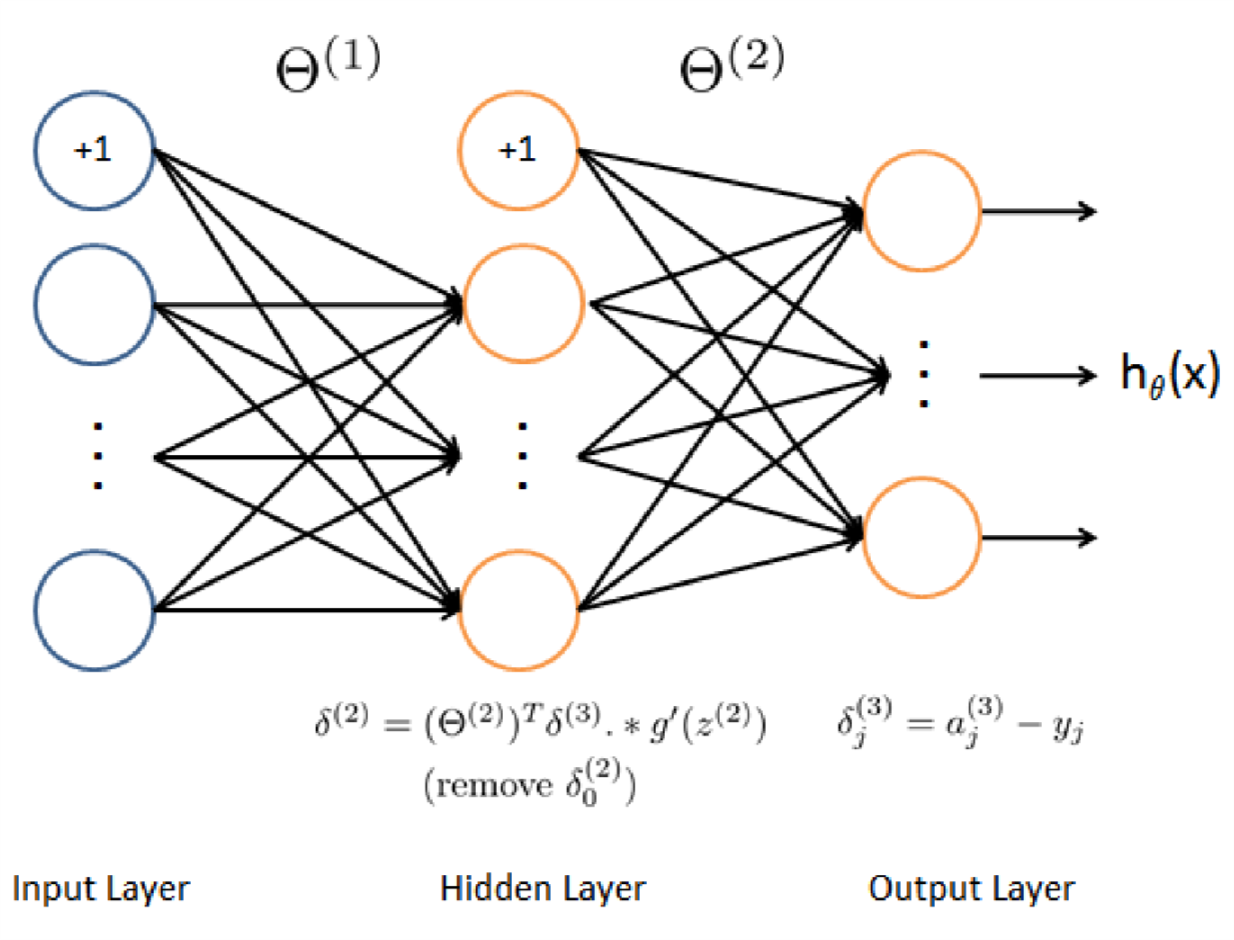
根据上图，我们需要循环处理所有样本，一次处理一个，所以一定会有一个 for t=1:m 。在第\(t\)次迭代的时候处理第\(t\)个样本。循环内的步骤为：

设定输入层的值为\(x^{t}\)，执行前向过程，计算\(z^{(2)},a^{(2)},z^{(3)},a^{(3)}\)。注意在计算过程中需要为\(a\)添加一个bias项。
对于层3中的每一个输出单元，设定\(\delta_{k}^{(3)} = ( a_{k}^{(3)} - y_{k})\) 其中\(y_{k}\)是二进制数表示当前的训练样本是不是第\(k\)类，如果是，则\(y_{k} = 1\)；如果当前样本属于其他类则\(y_{k}=0\)。
对隐藏层\(l=2\)，设定：\(\delta^{(2)} = (\Theta^{(2)})^{T}\delta^{(3)}.*g^{'}(z^{(2)})\)
从这个样本中累计梯度值。\[ \Delta^{(l)} = \Delta^{(l)} +\delta^{(l+1)}(a^{(l)})^{T} \] 注意要去掉\(\delta_{0}^{(2)}\)
获得梯度值：\[\frac{\partial}{\partial \Theta_{ij}^{(l)}}J(\Theta) = D_{ij}^{(l)} = \frac{1}{m}\Delta_{ij}^{(l)}\]

在matlab实现的过程中，也需要仔细核对相关变量的维度。由于我们在计算\(a^{(2)},a^{(3)},z^{(2)},z^{(3)}\)的过程中使用的是矢量计算，在计算\(\frac{\partial}{\partial \Theta_{ij}^{(l)}} J(\Theta)\)的过程中我们也可以使用全矢量计算。

%% calculate the theta gradient
delta3 = a3 - Y;
temp = Theta2;
temp(:,1) = 0;
Theta2_grad = delta3 * a2'./m + lambda./m*temp ;

delta2 = Theta2(:,2:end)'*delta3 .* sigmoidGradient(z2);
temp = Theta1;
temp(:,1) = 0;
Theta1_grad = delta2 * a1./m + lambda./m*temp;

需要注意的是在正则化过程中需要把\(\Theta\)中对应bias项的那些值去掉，在代码中我才用了置零处理。另外在计算\(\delta^{(2)}\)的过程中也需要把\(\Theta_{2}\)中与bias相关的项去掉。

神经网络要点理解

目录

1 损失函数及其正则化

2 后向传递算法