曲线拟合之matlab实现
1 回忆
在
中我们介绍了多项式曲线拟合问题并从多方面对其进行了分析，顺便引入了机器学习领域的一些关键术语。今天我们针对多项式曲线拟合问题做一些matlab试验。
1.1 数学模型
目标模型：
y(x,w)=w0+w1x+…+wMxM=M∑j=0wjxj均方误差函数：
E(w)=12N∑n=1{y(xn,w)−tn}2针对目标模型和均方误差函数的解w={wj}是一般线性方程：
M∑j=0Aijwj=Ti,i=0,…,M的解。其中Aij=∑Nn=1(xn)i+j，Ti=∑Nn=1(xn)itn 关于这个结论的证明过程详见 曲线拟合过程中的欠定过定问题 。
式 (3) 可以写成矩阵的形式，如下：
[A00…A0M⋮⋱⋮AM0…AMM][w0⋮wM]=[T0⋮TM]1.2 正则化过程
针对误差函数 (2)出现高阶模型的过拟合问题，对(2) 添加一个正则项会产生比较好的效果，如：
E(w)=12N∑n=1{y(xn,w)−tn}2+λ2‖w‖2其中‖w‖2=w20+ …w2M ，稍后我们会看到这种正则化方法对于克服过拟合问题非常有效。针对式 (5) 和式 (1) 的解可以写成如下形式的解：
M∑j=0(Aij+λδij)wj=Ti,i=0,…,M其中：
δij={1i=j0i≠j矩阵形式就是：
[A00−λ…A0M⋮⋱⋮AM0…AMM−λ][w0⋮wM]=[T0⋮TM]式~(8)和式 (4) 的区别在于，矩阵A的对角线上有一个λ的修正（或者叫做惩罚）。这样做的好处是求得的系数w不会太大。
2 matlab实现
2.1 画出y=sin(2πx)
首先我们画出y=sin(2πx)，这个函数的图像:
1: x = 0:0.01:1;%x 2: y = sin(2* pi * x); 3: figure 4: plot(x,y,'-r','linewidth',2),hold on;
结果如图1 所示：
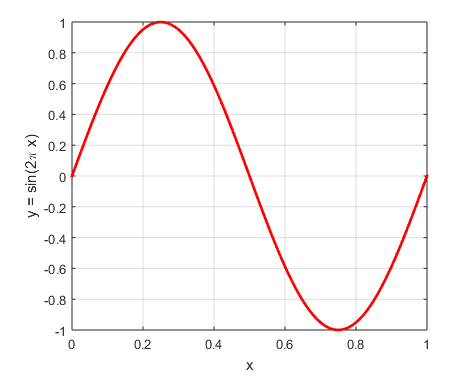
Figure 1: y=sin(2∗πx)
2.2 训练集合
然后给出一个训练集合，并画出这个集合的图像：
1: numTraining = 100; 2: xTraining = rand(1,numTraining); 3: noiseVariance = 0.5; 4: noise = noiseVariance *randn(1,numTraining); 5: yTraining = sin(2*pi*xTraining) + noise; 6: plot(xTraining,yTraining,'b+','linewidth',2),hold on;
和y=sin(2πx)画在一张图上，如图所示：
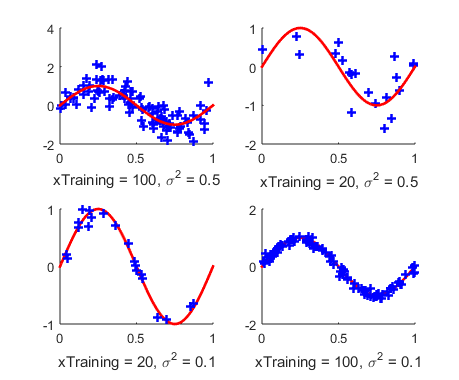
Figure 2: 训练集合
注意这里有两个地方可以做调整：1. 训练结合的数量 numTraining ；2. 噪声的方差 noiseVariance .不同的训练集合大小和方差会影响最终的训练效果。当然总体结论是：训练集合越大，方差越小，训练效果越好。
2.3 曲线拟合
曲线拟合的过程就是计算w的过程，首先我们观察式~(3) 的结果。我们把计算Ax=B的过程分为三步：
getAgetBA\B
这三步的代码：
1: %%find the A and B for Ax = B 2: A = getA(xTraining,modelOrder); 3: B = getB(xTraining,yTraining,modelOrder); 4: w = A\B'; 5: for i = 1:length(x) 6: yEstimation(i) = x(i).^(0:modelOrder ) * w ; 7: end
先是 getA
1: function A = getA(xTraining,modelOrder) 2: for i = 1:modelOrder + 1 3: for j = 1:modelOrder + 1 4: A(i,j) = sum(xTraining.^(i+j - 2)); 5: end 6: end 7: end
然后 getB
1: function B = getB(xTraining,yTraining,modelOrder) 2: for i = 1:modelOrder + 1 3: B(i) = sum(yTraining .* xTraining.^(i-1)); 4: end 5: end
我们给出 训练集合大小为20，模型阶数为9的训练结果：
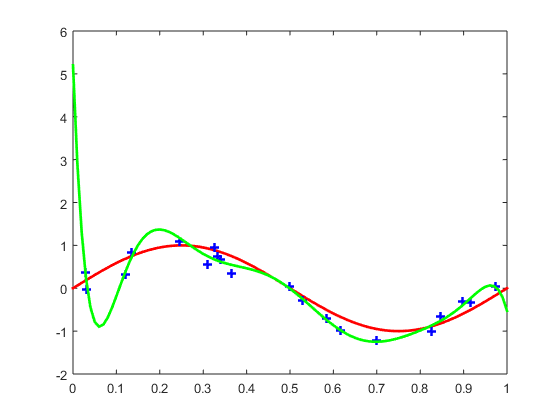
Figure 3: 训练集合大小为20，模型阶数为9的训练结果
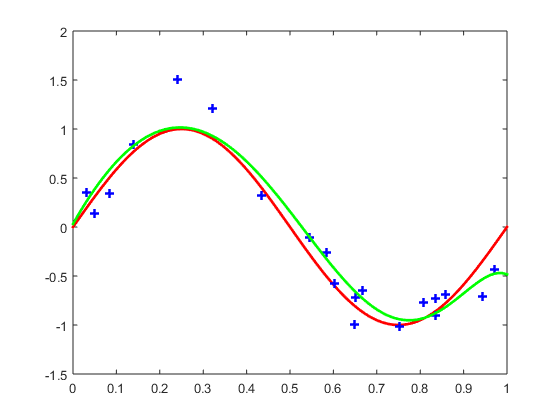
图中绿色曲线就是训练结果，可以看出来这个结果显然是过拟合了。我们给出来训练集合大小为20，模型结束为5的训练结果：
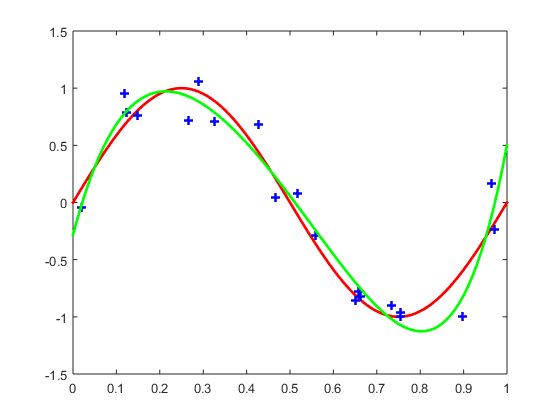
Figure 4: 训练集合大小为20，模型阶数为5的训练结果
