高斯随机变量
八卦一下 ,高斯随机变量不是高斯发现的,是一个叫亚伯拉罕⋅棣莫弗的数学家发现的。无论哪个发现的高斯随机变量,都不影响高斯随机变量在概率论中的重要地位。
1 定义
如果随机变量X的概率密度函数是:
f(x)=1√2πσ2e−(x−μ)22σ2,−∞<x<∞称这个随机变量服从参数为μ和σ2的高斯分布。稍后我们会发现μ和σ2在完全控制一个高斯变量,他们分别是该高斯变量的均值和方差。无论μ和σ2的值如何变化,高斯随机变量的图形始终是钟形。如图所示。
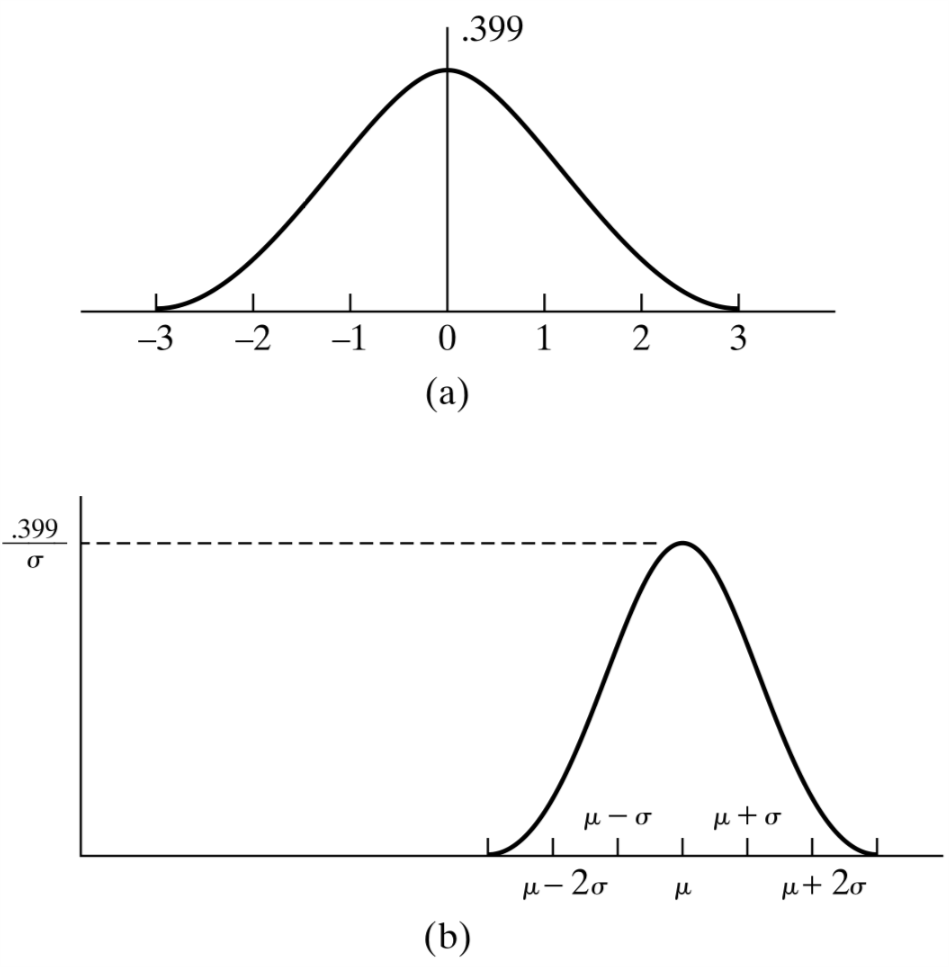
Figure 1: 高斯随机变量的形状
f(x)是一个概率密度函数,我们可以通过∫∞−∞f(x)dx=1来验证。
1√2πσ∫∞−∞e−(x−μ)22σ2dx=1变量替换,令y=x−μσ,式 (2)可以变为:
1√2π∫∞−∞e−y2/2dy=1即,我们需要证明
∫∞−∞e−y2/2dy=√2π这个积分非常有意思,令I=∫∞−∞e−y2/2dy,则:
I2=∫∞−∞e−y2/2dy∫∞−∞e−x2/2dx我们利用左边变换来求解上面的二重积分,令:
x=rcosθy=rsinθ则dxdy=rdθdr,所以有:
I2=∫∞0∫2π0e−r2/2rdθdr=2π∫∞0re−r2/2dr=2π因此I=√2π
2 正态分布的性质
2.1 期望和方差
先从标准正态分布的期望和方差开始,由于:
E[X]=1√2π∫∞−∞xe−x2/2dx=0分部积分,我们得到Var(X)=1
2.2 正态分布的线性函数
如果X是一个服从参数为μ和σ2的正态分布的随机变量,那么aX+b也服从正态分布,且参数为aμ+b和a2σ2。设FY为Y的分布函数,则:
FY(x)=P{Y≤x}=P{aX+b≤x}=P{X≤x−ba}=Fx(x−ba)其中FX(x)为X的分布函数,求导可得Y的密度函数:
fY(x)=1afx(x−ba)=1√2πaσe−(x−ba−μ)22σ2=1√2πaσe−(x−b−aμ)22(aσ)2即,假设X是均值为μ方差为σ2的高斯变量,则aX+b则是一个均值为aμ+b方差为a2σ2的高斯变量。这个结论的一个重要应用是,如果X是一个参数为μ,σ2的正态随机变量,那么Z=X−aσ是一个参数为(0,1)的正态随机变量。参数为(0,1)的正态随机变量成为标准正态随机变量。
3 棣莫弗拉普拉斯极限定理
概率论中一个重要的结论就是棣莫弗拉普拉斯极限定理,它表明当n充分大时,参数为n,p的二项随机变量可以由正态随机变量来近似,其中正态随机变量的期望和方差与二项随机变量的期望和方差相同。更一般的表述:我们可以将二项随机变量标准化,先减去均值np,然后再除以标准差√np(1−p),那么经过标准化后的随机变量的分布函数当n→∞时收敛于标准正态分布。
在n次独立重复试验中,设每次成功的概率为p,记成功的总次数为Sn,那么对于任意a<b有:当(n→ ∞)时,
P{a≤Sn−np√np(1−p)≤b}→Φ(b)−Φ(a)现在,二项分布有两种可能的近似:当n较大p较小时,泊松分布 是一个很好的近似;另外,可以证明,当np(1−p)较大时,正态分布近似的效果很好。一般情况下,当np(1−p)≥10时,正态近似就非常好。

