曲线拟合之最大斯然估计和最小二乘法
之前,我们讨论过关于曲线拟合的一些概念,提到了均方误差函数和贝叶斯估计 , 并在一篇博文中介绍了 matlab 实现。今天,我们讨论通过最小二乘法对最大斯然估计进行深入的挖掘。
1 问题模型
假设目标变量是t,其可以通过如下模型生成:
t=y(x,w)+ϵ其中,ϵ是高斯白噪,均值为 0,方差是β。所以我们可以把t的概率密度函数表示为:
p(t|x,w,β)=N(t|y(x,w),β−1)2 问题分析:最大化似然函数和最小化平方和误差函数的等效性
如果我们的损失函数是均方误差,那么对于一个新的输入x,最优的预测是基于目标变量的条件均值。针对式~(2),我们有:
E[t|x]=∫tp(t|x)dt=y(x,w)注意,高斯白噪的假设使得给定x的t的条件均值是各向一致的。
现在考虑输入的数据集合X={x1,…,xN},对应的目标变量是t1,…,tN。我们假设数据集合是从式~(2)所示分布中采样得到的。所以,关于X的最大斯然估计为:
p(t|X,w,β)=N∏n=1N(tn|wTϕ(xn),β−1)注意,这里我们假定 y(x,w)=wTϕxn
对式~(5)稍作变形,有:
lnp(t|w,β)=N2ln(β)−N2ln(2π)−βED(w)其中,
ED(w)=12N∑n=1{tn−wTϕ(xn)}2我们发现,优化基于高斯白噪的斯然函数和最小化平方和误差函数是等效的。通过对~(6)进行求导,有:
∇lnp(t|w,β)=N∑n=1{tn−wTϕ(xn)}ϕ(xn)T令式~(8)等于零,
0=N∑n=1tnϕ(xn)T−wT(N∑n=1ϕ(xn)ϕ(xn)T)继而有:
wML=(ΦTΦ)−1ΦTt这个解是最小二乘问题的解。这里Φ是N×M的矩阵:
Φ=[ϕ0(x1)ϕ1(x1)…ϕM−1(x1)ϕ0(x2)ϕ1(x2)…ϕM−1(x2)⋮⋮⋱⋮ϕ0(xN)ϕ1(xN)…ϕM−1(xN)]其中,(ΦTΦ)−1ΦT是Φ的 Moore-Penrose 伪逆。这个伪逆是逆的推广。当Φ是方阵且可逆时,这个结果就直接等于Φ−1
此刻,我们再分析w0。重写ED(w):
ED(w)=12N∑n=1{tn−w0−M−1∑j=1wjϕj(xn)}2对w0求导,可得:
w0=ˉt−M−1∑j=1wj¯ϕj其中:
ˉt=1NN∑n=1tn,¯ϕj=1Nϕj(xn)所以,w0补充了训练集合中目标值的均值与基函数之间的差值。
另外,我们可以对式~(6)求β的导数,得β:
1βML=1NN∑n=1{tn−wTMLϕ(xn)}2我们看到噪声精度的倒数是目标值在回归函数周围的方差。
3 最小二乘的几何意义
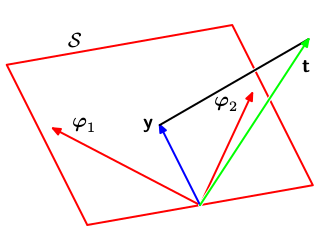
图 1: 最小二乘的几何意义
考虑N维空间,t是其中一个矢量。每一个基函数ϕj(xn)取N个训练集合中的值也可以视作一个矢量,标记为φj,如图 1所示。注意φj对应Φ的第j列。如果基函数的个数M小于训练集合的点数N,那么M个矢量ϕj(xn)张成一个M维的空间S。我们定义y是一个N维向量其第n个坐标为y(xn,w)。因为y是φj 的线性组合。所以,y可以在M维空间S的任意位置。式~(7)是y和t的欧几里得距离。所以w的最小二乘解对应着S中距离t最近的y。从图 1 可以看出这个解对应着t向S的各个坐标系投影。
在实际应用中,直接求解ΦTΦ的逆比较困难(因为,这个矩阵的维度比较大),所以一些数学技巧比如 SVD 分解经常会被用到。

