内积与范数
1 内积
x=(x1,…,xn)∈Rn的范数为:
||x||=√x21+…+x2n范数在Rn上不是线性的,为了把线性引入讨论,定义点积:
对于x,y∈Rn,x和y的点积x⋅y定义为:
x⋅y=x1y1+…xnyn其中x=(x1,…,xn),y=(y1,…,yn)
注意Rn中两个向量的点积是一个数。对所有的x∈Rn,均有x⋅x=||x||2,Rn上的点积具有如下性质:
- 对所有x∈Rn,均有x⋅x≥0
- x⋅x=0,当且仅当x=0
- 对于固定的y∈Rn,Rn到R的将x∈Rn变为x⋅y的映射是线性的。
- 对所有x,y∈Rn,有x⋅y=y⋅x
内积是点积的推广。定义内积就是抽象化点积的过程:
V上的内积就是一个函数,把V中的元素的每个有序对u,v都映成一个数⟨u,v⟩ 并且具有以下性质:
- 对所有的v∈V,有⟨v,v⟩≥0
- ⟨v,v⟩=0,当且仅当v=0
- 对所有u,v,w∈V,均有⟨u+v,w⟩=⟨u,w⟩+⟨v,w⟩
- 对所有λ∈F和所有u,v∈V,有⟨λu,v⟩=λ⟨u,v⟩
- 对所有u,v∈V,有⟨u,v⟩=¯⟨v,u⟩
Fn上的欧几里得内积定义为:
⟨(w1,…,wn),(z1,…,zn)⟩=w1¯z1+…+wn¯zn若c1,…,cn均为正数,则可以定义Fn上的内积:
⟨(w1,…,wn),(z1,…,zn)⟩=c1w1¯z1+…+cnwn¯zn在定义区间[−1,1]上的实值连续函数构成的向量空间上可定义内积如下:
⟨f,g⟩=∫1−1f(x)g(x)dx在P(R)上可定义内积如下:
⟨p,q⟩=∫∞0p(x)q(x)e−xdx内积空间就是带有内积的向量空间 V
内积空间最重要的例子是Fn,当我们说Fn是内积空间的时候,我们总假设采用的是欧几里得内积。
- 对每个确定的u∈V,将v变为v,u的函数是V到F的线性映射。
- 对每个u∈V,均有⟨0,u⟩=0
- 对每个u∈V,均有⟨u,0⟩=0
- 对所有u,v,w∈V均有⟨u,v+w⟩=⟨u,v⟩+⟨u,w⟩
- 对所有λ∈F和所有u,v∈V均有⟨u,λv⟩=ˉλ⟨u,v⟩
2 范数
对于v∈V,v的范数‖v‖=√⟨v,v⟩
若(z1,…,zn)∈Fn,则:
‖(z1,…,zn)‖=√|z1|2+ …+|zn|2在[−1,1]上的实值连续函数构成的向量空间中有:
‖f‖=√∫1−1(f(x))2dx范数的基本性质:
设v∈V
- ‖v‖=0 当且仅当v=0
- 对所有λ∈F均有‖λv‖=|λ|‖v‖
通常,处理范数的平方要比直接处理范数更容易。
两个向量u,v∈V是正交的,如果⟨u,v⟩=0
若u,v是R2中的非零向量,则:
⟨u,v⟩=‖u‖‖v‖cosθ其中θ是u和v的夹角,显然在平面几何的意义下,正交意味着垂直。
- 0正交与V中的任意向量。
- 0是V中唯一一个与自身正交的向量。
设u和v是V中的正交向量,则‖u+v‖2=‖u‖2+‖v‖2
设u,v∈V,且v≠0,我们想把u写成v的标量倍加上一个正交与v的向量w。如图1所示:
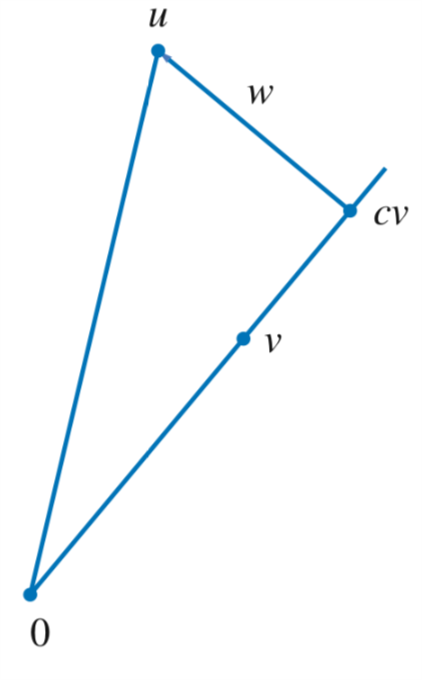
Figure 1: 正交分解
为了揭示如何将u写成v的标量倍加上一个正交于v的向量,令c∈F表示一个标量,则: u=cv+(u−cv)
设u,v∈V且v≠0,令c=⟨u,v⟩‖v‖2,w=u−⟨u,v⟩‖v‖2v则⟨w,v⟩=0,且u=cv+w
设u,v∈V,则 |⟨u,v⟩|≤‖u‖‖v‖,等号成立当且仅当u,v之间存在标量倍的关系。
我们把u分解为: u=w+⟨u,v⟩‖v‖2v
柯西施瓦茨不等式的例子
若x1,…,xn,y1,…,yn∈R,则:
|x1y1+…xnyn|2≤(x21+…x2n)(y21+…+y2n)若f,g均为[−1,1]上的实值连续函数,则:
|∫1−1f(x)g(x)dx|2≤(∫1−1(f(x))2dx)(∫−1−1(g(x))2dx)设u,v∈V,则‖u+v‖≤‖u‖+‖v‖,等号成立当且仅当u,v之一是另一个的标量倍。
所以 ‖u+v‖≤‖u‖+‖v‖
设u,v∈V,则‖u+v‖2+‖u−v‖2=2(‖u‖2+‖v‖2)

