通信系统中的随机过程
在 一维随机游动 的例子中，我们讨论了参数离散取值离散的随机过程，今天，给出一个参数连续取值离散的随机过程。
设有一个脉冲数字通信系统，它传送的信号是脉冲宽度为T0的脉冲信号，每隔T0送出一个脉冲。脉冲幅度ξ(t)是一个随机变量，它可取四个值{−2,−1,1,2}，且取这四个值的概率是相同的，即：
P(ξ(t)=2)=P(ξ(t)=1)=P(ξ(t)=−1)=P(ξ(t)=−2)=1/4不同周期内脉冲幅度是相互统计独立的，脉冲的起始时间相对于原点t=0的时间差u为均匀分布在0,T0内的随机变量。试求在两个时刻t1,t2该随机过程ξ(t)所取值ξ(t1),ξ(t2)的二维联合概率密度。
首先，给出一个该脉冲数字通信数字信号的一个典型样本函数。如图1所示
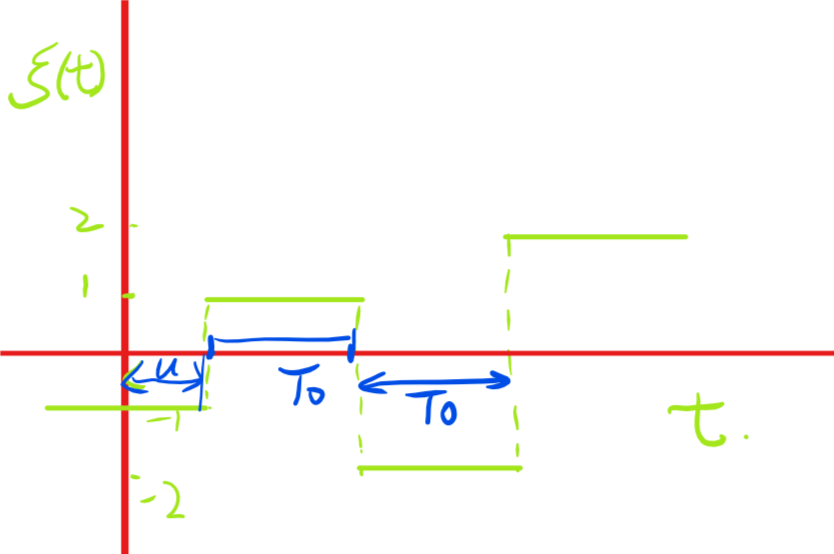
Figure 1: 脉冲信号的典型样本函数
在时间轴上固定两个时刻t1,t2。首先要研究的问题时t1,t2是否处于一个脉冲内。设事件c表示t1,t2处于不同的脉冲，它的逆事件cc表示t1,t2处于同一脉冲周期内。
当|t1−t2|>T0时，事件c是必然事件，此时，P(c)=1,P(cc)=0,;
当|t1−t2|≤T0时，t1,t2有可能在同一脉冲内，也有可能处于两个不同的脉冲内。设θ为t1所在的脉冲的起始时刻。由于脉冲的起始时间相对于原点t=0的时间差u均匀分布于(0,T0)内，而且该信号为等脉宽的脉冲信号，脉宽均匀为T0。则θ也是均匀分布的随机变量，θ可视为均匀分布于[t1−T0,t1]内的随机变量。图2给出了θ的概率密度和t1,t2,θ的关系图。
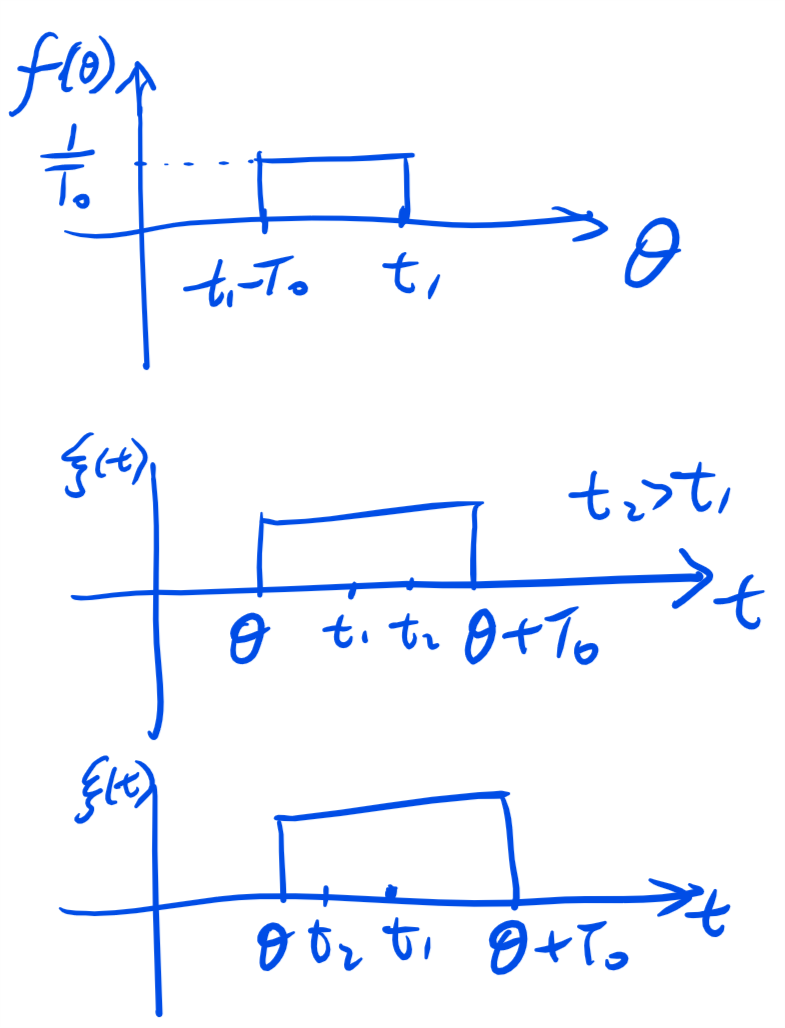
Figure 2: t1,t2,θ关系图
如果t1<t2，则：
P(cc)=P(t2<θ+T0)=P(θ>t2−T0)=1−P(θ<t2−T0)=1−1T0∫t2−T0t1−T0dθ=1−t2−t1T0如果t2<t1 ，则：
P(cc)=P(t2>θ)=1T0∫t2t1−T0dθ=1−t1−t2T0因此：
P(cc)=1−|t1−t2|T0P(c)=|t1−t2|T0根据全概率公式：
fξt1,ξt2(x1,x2)=fξt1,ξt2,c(x1,x2|c)P(c)+fξt1,ξt2,cc(x1,x2|cc)P(cc)又因为不同周期内脉冲幅度是相互统计独立的随机变量，于是：
fξt1,ξt2,c(x1,x2|c)=∑i={−2,−1,1,2}14δ(x1−i)∑k={−2,−1,1,2}14δ(x2−k)如果t1,t2处于同一周期，则ξ(t1=ξ(t2))，这时:
fξt1,ξt2|cc=∑i={−2,−1,1,2}14δ(x1−i)δ(x2−i)综上有： 当|t1−t2|≤T0时：
fξt1,ξt2(x1,x2)=∑i={−2,−1,1,2}14δ(x1−i)∑k={−2,−1,1,2}14δ(x2−k)|t1−t2|T0+∑i={−2,−1,1,2}14δ(x1−i)δ(x2−i)(1−|t1−t2|T0)当|t1−t2|≥T0时：
fξt1,ξt2(x1,x2)=∑i={−2,−1,1,2}14δ(x1−i)∑k={−2,−1,1,2}14δ(x2−k)在这个题目中，全概率公式是主线，如何进行概率空间的划分是解决这个问题的关键。